class: center, middle, inverse, title-slide .title[ # Centrality in Social Networks ] .author[ ### David Garcia <br><br> <em>ETH Zurich, Chair of Systems Design</em> ] .date[ ### Social Data Science ] --- layout: true <div class="my-footer"><span>David Garcia - Social Data Science - ETH Zurich, Chair of Systems Design</span></div> --- # Who is the most important in a network? .pull-left[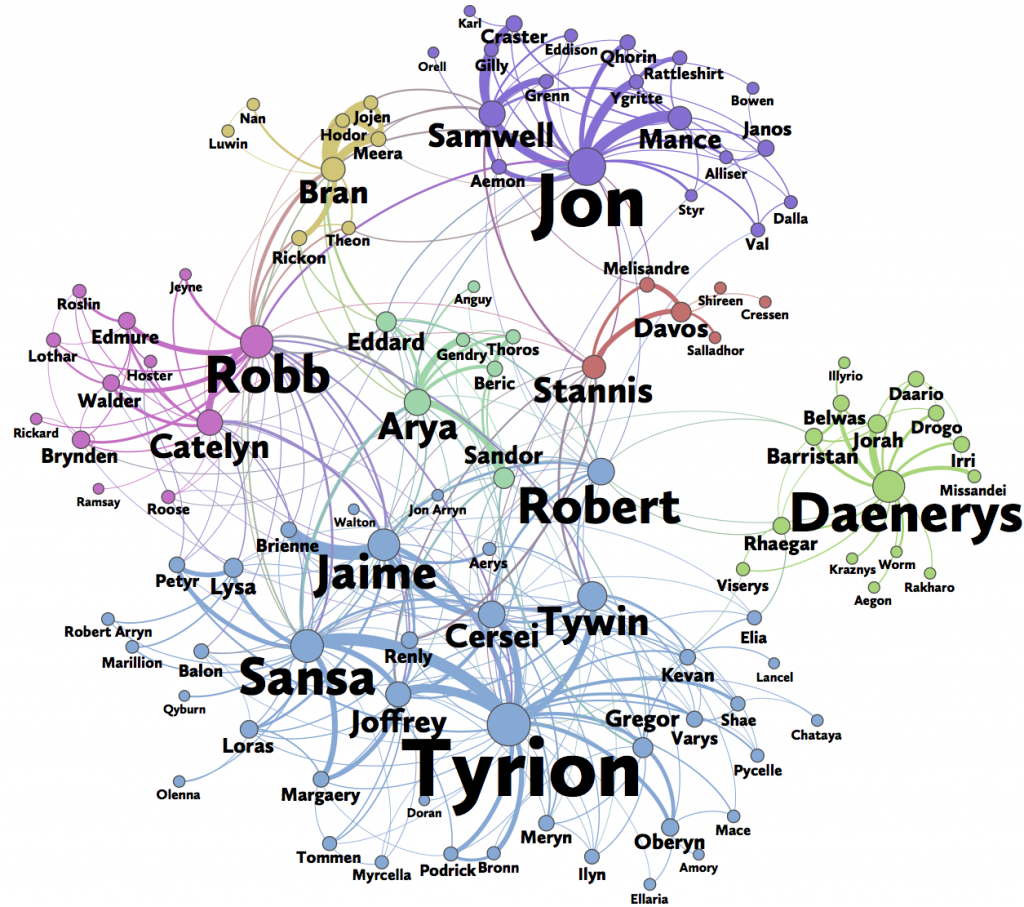] .pull-right[ - Network based on Game of Thrones books - Nodes are characters - Edges are weighted according to the number of times the are mentioned within 15 words **Pair up and discuss:** - Who is the most important character? - Why? Who else could be? [Data on Github](https://github.com/mathbeveridge/asoiaf) and [Image source](https://predictivehacks.com/social-network-analysis-of-game-of-thrones/) ] --- # The concept of centrality Social network analysis can be used to measure the importance of a person as a function of the social structure of a community or organization. In social networks, **centrality** measures this kind of structural importance of the node of a person. There are various centrality measures that stem from different kinds of structural importance. In this topic you will learn about three centrality measures: 1. Degree centrality 2. Betweenness centrality 3. Closeness centrality + Coreness centrality (in social resilience topic) --- # Degree centrality <div style="float:right"> <img src="networkDirected.png" alt="Network example." width=400px/> </div> A node's **degree centrality** measures the number of links connected to it. In directed networks: - **in-degree** `\(d_{in}(i)\)` that is the number of edges ending in `\(i\)`, i.e. `\((j,i)\)` - **out-degree** `\(d_{out}(i)\)` that is the number of edges leaving from `\(i\)`, i.e. `\((i,j)\)` `\(d_{in}(c) = 1\)` and `\(d_{out}(c) = 2\)` If importance on Twitter is the number of followers of an account, in-degree centrality is a way to measure it. --- # Betweenness Centrality <div style="float:right"> <img src="undirNetworkBtw.png" alt="Network betweenness example." width=400px/> </div> Sometimes the importance of a person is quantified as the number of shortest paths between two other people that pass through this person. In this case, **betweenness** centrality measures importance: `$$C_B(i) = \sum_{s \neq i, t \neq i} n_i(s,t)$$` Where `\(n_i(s,t)\)` is the number of shortest paths from `\(s\)` to `\(t\)` that pass through `\(i\)`. Example: `\(C_B(b) = 16\)` --- # Closeness Centrality <div style="float:right"> <img src="undirNetworkBtw.png" alt="Network betweenness example." width=400px/> </div> Sometimes the most important people in a group are the ones that can reach everyone with the least effort. In these cases, **closeness** centrality measures importance as: `$$C_C(i) = \frac{n-1}{\sum_{j\neq i} dist(i,j)}$$` Where `\(dist(i, j)\)` is the distance from `\(i\)` to `\(j\)` and `\(n\)` is the number of nodes in the network. Example: `\(C_C(d)=0.75\)` --- ## Neocortex Size as a limit to degree centrality  --- ## Dunbar's number in Online Social Networks .center[] --- # Dunbar's number on Twitter .center[]